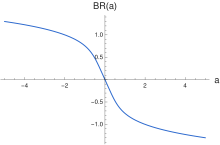
 实系数下布灵根式的图
实系数下布灵根式的图
布灵根式(英语:Bring radical)或是超根式(英语:ultraradical)是代数术语。布灵根式不是一般意义下的根式(n次方根,或“单位根”),复数a的布灵根式可以用 表示,是指以下五次方程的解
表示,是指以下五次方程的解

对应一复数a的布灵根式,是上述方程式五个解中的一个(因此是多值函数)一般会选择布灵根式的根,使得实数的布灵根式为正值,而且在实数线附近可解析。布灵根式在复平面上有四个分支点,因此无法定义为复数平面上的连续函数,其连续域需要排除其分支切割。
布灵根式是由厄兰·塞缪尔·布灵发明的,乔治·杰拉德证明有些五次方程可以用n次方根及布灵根式求解,因此可以用在一些五次方程的闭合形式解中。
此条目中。a的布灵根式表示为 。若a是实数,此函数是奇函数、单调递减且无界,在
。若a是实数,此函数是奇函数、单调递减且无界,在 很大时,其渐近行为
很大时,其渐近行为 。
。
布灵根式的泰勒级数,以及以广义超几何函数的表示式可以用以下方式推导。方程 可以写成
可以写成 ,若令
,若令 ,想要的解是
,想要的解是 ,因为
,因为 是奇函数。
是奇函数。
 的级数可以用
的级数可以用 泰勒级数(就是
泰勒级数(就是 )的反算来得,令
)的反算来得,令

其中系数的绝对值形成整数数列线上大全中的A002294。数列的收敛半径为![{\displaystyle 4/(5\cdot {\sqrt[{4}]{5}})\approx 0.53499.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6700ff821af8676bf88bdcecf304b7594546897) 。
。
布灵根式的超几何函数形式可以写成[1]:
















![{\displaystyle 4/(5\cdot {\sqrt[{4}]{5}})\approx 0.53499.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6700ff821af8676bf88bdcecf304b7594546897)
