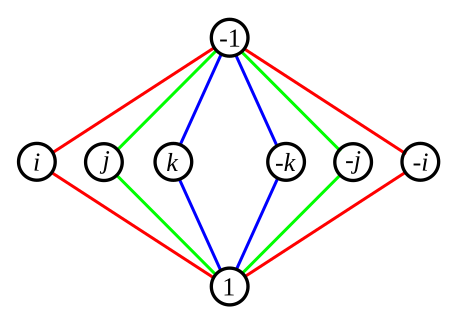
 Q的环图。每一种颜色代表连结至单位元(1)之任一元素的次方。例如,红色的环反映了
Q的环图。每一种颜色代表连结至单位元(1)之任一元素的次方。例如,红色的环反映了 、
、 和
和  ,亦反映了
,亦反映了 、
、 和
和  。
。
在群论里,四元群  (Quaternion Group) 是指一个阶为8的非交换群,常被简写为
(Quaternion Group) 是指一个阶为8的非交换群,常被简写为  ,且用乘法的形式表示。包含下列8个元素:
,且用乘法的形式表示。包含下列8个元素:

其中, 代表单位元素,且
代表单位元素,且  。对于每个元素
。对于每个元素  ,有
,有  的关系。另外,
的关系。另外,

 的凯莱表如下:
的凯莱表如下:
|
1 |
i |
j |
k |
−1 |
−i |
−j |
−k
|
| 1
|
1 |
i |
j |
k |
−1 |
−i |
−j |
−k
|
| i
|
i |
−1 |
k |
−j |
−i |
1 |
−k |
j
|
| j
|
j |
−k |
−1 |
i |
−j |
k |
1 |
−i
|
| k
|
k |
j |
−i |
−1 |
−k |
−j |
i |
1
|
| −1
|
−1 |
−i |
−j |
−k |
1 |
i |
j |
k
|
| −i
|
−i |
1 |
−k |
j |
i |
−1 |
k |
−j
|
| −j
|
−j |
k |
1 |
−i |
j |
−k |
−1 |
i
|
| −k
|
−k |
−j |
i |
1 |
k |
j |
−i |
−1
|
需要特别留意,这个群不是交换群,例如  。
。 有着汉弥尔顿群较不常见的性质:每一个
有着汉弥尔顿群较不常见的性质:每一个  的子群都是其正规子群,但这个群不是交换的。每一个汉弥尔顿群都会含有一个或多个
的子群都是其正规子群,但这个群不是交换的。每一个汉弥尔顿群都会含有一个或多个  。
。
在抽象代数里,可以造出一个其基底为  的四维实向量空间,并使用上面的乘法表和分配律来形成一个结合代数,称为一个四元数的除环。需要注意的是,这不是在
的四维实向量空间,并使用上面的乘法表和分配律来形成一个结合代数,称为一个四元数的除环。需要注意的是,这不是在  上的群代数(其应该是8维的)。相反地,也可以先由四元数开始,再“定义”出由八个元素
上的群代数(其应该是8维的)。相反地,也可以先由四元数开始,再“定义”出由八个元素  所组成之乘法子群作为四元群。
所组成之乘法子群作为四元群。
 都是
都是  中阶为4的元素,任意选择其中两个就可以生成出整个群。
中阶为4的元素,任意选择其中两个就可以生成出整个群。 有着下列的展现 (presentation):
有着下列的展现 (presentation):

其中可以取  、
、 及
及  。
。
 的中心及交换子群为
的中心及交换子群为  。其商群
。其商群  同构于克莱因四元群 (Klein four-group)
同构于克莱因四元群 (Klein four-group)  。而
。而  的内自同构群 (Inner Automorphism Group) 同构于
的内自同构群 (Inner Automorphism Group) 同构于  同余其中心,且因此也会同构于克莱因四元群。
同余其中心,且因此也会同构于克莱因四元群。 的自同构群会同构于对称群
的自同构群会同构于对称群  。
。 的外自同构群因此为
的外自同构群因此为  。
。
四元群  亦可视为是作用于在有限体
亦可视为是作用于在有限体  上之二维向量空间的八个非零元素。关于其图像,请见图像化GL(2,p)(页面存档备份,存于互联网档案馆)。
上之二维向量空间的八个非零元素。关于其图像,请见图像化GL(2,p)(页面存档备份,存于互联网档案馆)。
一个群若被称为广义四元群,则表示其有一个展现

其中  为整数。这个群的阶为
为整数。这个群的阶为  。原本的四元群为
。原本的四元群为  时的特例。广义四元群可以被理解为单位四元数的子群,其生成元 (generator) 为
时的特例。广义四元群可以被理解为单位四元数的子群,其生成元 (generator) 为


广义四元群是双循环群此一更大类型的一类。广义四元群有着每个交换子群都是循环群的性质。可证明一具有此性质(每个交换子群都是循环群)的有限p-群若不是循环群就是广义四元群。



































