勞侖茲因子是一個出現在狹義相對論中的速記因子,得名於荷蘭物理學家亨德里克·勞侖茲,被用於計算時間膨脹、長度收縮、相對論質量等相對論效應。
勞侖茲因子定義為:

其中
一些作者另外定義了勞侖茲因子的倒數:[1]

可用於速度相加推導。
相對論性條件(近光速)下,物體的總能量 與動量
與動量 可以通過勞侖茲因子
可以通過勞侖茲因子 簡單寫為:
簡單寫為:


其中 為靜質量。
為靜質量。
在四維向量描述下,能-動向量則成為:

和牛頓力學的三維動量 定義相似。
定義相似。
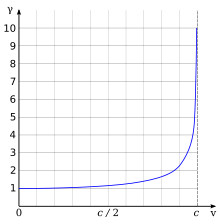 勞侖茲因子與速度的關係。速度為零時勞侖茲因子為1,速度
勞侖茲因子與速度的關係。速度為零時勞侖茲因子為1,速度 時勞侖茲因子趨於無窮大。
時勞侖茲因子趨於無窮大。
下表中,最左欄為以c為單位的速率;中間欄顯示相應的勞侖茲因子;最右欄為勞侖茲因子的倒數。以粗體字顯示者為精確值。
| 速率(c為單位) |
勞侖茲因子 |
倒數
|
 |
 |

|
| 0.000 |
1.000 |
1.000
|
| 0.050 |
1.001 |
0.999
|
| 0.100 |
1.005 |
0.995
|
| 0.150 |
1.011 |
0.989
|
| 0.200 |
1.021 |
0.980
|
| 0.250 |
1.033 |
0.968
|
| 0.300 |
1.048 |
0.954
|
| 0.400 |
1.091 |
0.917
|
| 0.500 |
1.155 |
0.866
|
| 0.600 |
1.250 |
0.800
|
| 0.700 |
1.400 |
0.714
|
| 0.750 |
1.512 |
0.661
|
| 0.800 |
1.667 |
0.600
|
| 0.866 |
2.000 |
0.500
|
| 0.900 |
2.294 |
0.436
|
| 0.990 |
7.089 |
0.141
|
| 0.999 |
22.366 |
0.045
|
當速度遠小於光速(非相對論性條件下),即 ,則
,則 趨近於0,而
趨近於0,而 趨近於1,回到傳統的牛頓力學描述。
趨近於1,回到傳統的牛頓力學描述。
- ^ Yaakov Friedman, Physical Applications of Homogeneous Balls, Progress in Mathematical Physics 40 Birkhäuser, Boston, 2004, pages 1-21.

















