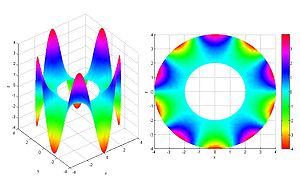
 定義在環形上的拉普拉斯方程上的一個解。拉普拉斯算子是橢圓算子的最有名的一個例子。
定義在環形上的拉普拉斯方程上的一個解。拉普拉斯算子是橢圓算子的最有名的一個例子。
橢圓算子是數學偏微分方程理論中的一類微分算子,它是拉普拉斯算子的泛化。橢圓算子定義為所有最高階導數的係數為正的微分算子,這意味着算子沒有實的特徵方向。
橢圓算子是典型的位勢論,並且它們頻繁地出現在靜電學和連續介質力學中。橢圓算子的正則性意味着它的解通常是光滑函數(如果算子的係數是光滑的)。雙曲方程和拋物方程的穩定解通常要求解橢圓方程。
 域
域 上的線性微分算子
上的線性微分算子

被稱為橢圓算子,如果對任意 ,任意非零
,任意非零 滿足
滿足
 。
。
在許多應用中僅滿足上述條件還遠遠不夠,當 時可用一致橢圓條件代替它:
時可用一致橢圓條件代替它:
 其中C是正常數。注意到橢圓性只依賴於最高階項。
其中C是正常數。注意到橢圓性只依賴於最高階項。
非線性算子

是橢圓算子如果它關於 的一階泰勒展開式在任意一點處都是線性橢圓算子。
的一階泰勒展開式在任意一點處都是線性橢圓算子。
為了說明問題,我們選取二階偏微分算子形式,

其中 .如果滿足高階項係數矩陣x
.如果滿足高階項係數矩陣x

為正定實係數對稱矩陣,則這樣的算子叫做橢圓算子。















