
此條目頁的主題是數學當中的一種函數或運算。關於電子系統設計與信號傳輸中的差分傳輸,請見「
差分信號」。
差分,又名差分函數或差分運算,一般是指有限差分(英語:Finite difference),是數學中的一個概念,將原函數  映射到
映射到  。差分運算,相應於微分運算,是微積分中重要的一個概念。
。差分運算,相應於微分運算,是微積分中重要的一個概念。
差分分為前向差分和逆向差分。
函數的前向差分通常簡稱為函數的差分。對於函數 ,如果在等距節點:
,如果在等距節點:


則稱 ,函數在每個小區間上的增量
,函數在每個小區間上的增量 為
為 一階差分。[1]
一階差分。[1]
在微積分學中的有限差分(finite differences),前向差分通常是微分在離散的函數中的等效運算。差分方程的解法也與微分方程的解法相似。當 是多項式時,前向差分為Delta算子(稱
是多項式時,前向差分為Delta算子(稱 為差分算子[2]),一種線性算子。前向差分會將多項式階數降低 1。
為差分算子[2]),一種線性算子。前向差分會將多項式階數降低 1。
對於函數 ,如果:
,如果:

則稱 為
為 的一階逆向差分。
的一階逆向差分。
一階差分的差分為二階差分,二階差分的差分為三階差分,其餘類推。記:
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805521ccbfe6baf45085b5499093e5362c33cb2d) 為
為 的
的 階差分。
階差分。
如果
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805521ccbfe6baf45085b5499093e5362c33cb2d)
|
\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dec48afb9723d70eb6d843de94c7a5069370bfb)
|
|
|
-\Delta ^{n-1}[f](x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e507cab6c570c0f32063759cd143e826adbb9e61)
|
根據數學歸納法,有
=\sum _{i=0}^{n}{n \choose i}(-1)^{n-i}f(x+i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/378a9d98e057cb2afcfe03160ed26d7598cf4586)
其中, 為二項式係數。
為二項式係數。
特別的,有
=f(x+2)-2f(x+1)+f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/002e6ddd14e4ec8068b1d97640ed68e91d1012e3)
前向差分有時候也稱作數列的二項式變換
對比解析函數中的微分的屬性,差分的性質有:

- 線性:如果
 和
和  為常數,則有
為常數,則有

- 乘法定則(此處步長
 ):
):




- 或




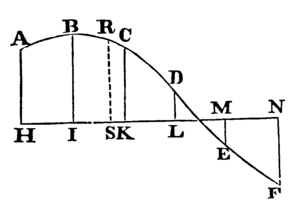 《自然哲學的數學原理》的第三編「宇宙體系」的引理五的圖例。這裡在橫坐標上有6個點H,I,K,L,M,N,對應著6個值A,B,C,D,E,F,生成一個多項式函數對這6個點上有對應的6個值,計算任意點S對應的值R。牛頓給出了間距為單位值和任意值的兩種情況。
《自然哲學的數學原理》的第三編「宇宙體系」的引理五的圖例。這裡在橫坐標上有6個點H,I,K,L,M,N,對應著6個值A,B,C,D,E,F,生成一個多項式函數對這6個點上有對應的6個值,計算任意點S對應的值R。牛頓給出了間距為單位值和任意值的兩種情況。
牛頓插值公式也叫做牛頓級數,由「牛頓前向差分方程」的項組成,得名於伊薩克·牛頓爵士,最早發表為他在1687年出版的《自然哲學的數學原理》中第三編「宇宙體系」的引理五[3],此前詹姆斯·格雷果里於1670年和牛頓於1676年已經分別獨立得出這個成果。一般稱其為連續泰勒展開的離散對應。
當 值間隔為單位步長
值間隔為單位步長 時,有:
時,有:
+{\frac {x-a-1}{2}}\left(\Delta ^{2}[f](a)+\cdots \right)\right]\\&=f(a)+\sum _{k=1}^{n}\Delta ^{k}[f](a)\prod _{i=1}^{k}{\frac {[(x-a)-i+1]}{i}}\\&=\sum _{k=0}^{n}{x-a \choose k}~\Delta ^{k}[f](a)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaaae992f781f01dc21b5796c9d397a09060b194)
這成立於任何多項式函數和大多數但非全部解析函數。這裡的表達式

是二項式係數,其中的 是「下降階乘冪」(另一種常見的標記法為
是「下降階乘冪」(另一種常見的標記法為 ),空積
),空積 被定義為
被定義為 。這裡的
。這裡的}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bc739bf70fe5e7a770c261da81fe064a8e5f261) 是「前向差分」的特定情況,即間距
是「前向差分」的特定情況,即間距 。
。
為了展示牛頓的這個公式是如何使用的,舉例數列 1, 4, 9,16...的前幾項,可以找到一個多項式重新生成這些值,首先計算一個差分表,接著將對應於x0(標示了下劃線)的這些差分代換入公式,

對於x值間隔為非一致步長的情況,牛頓計算均差,在間隔一致但非單位量時,即上述前向差分的一般情況,插值公式為:
+{\frac {x-a-h}{2h}}\left(\Delta _{h}^{2}[f](a)+\cdots \right)\right]\\&=f(a)+\sum _{k=1}^{n}{\frac {\Delta _{h}^{k}[f](a)}{k!h^{k}}}\prod _{i=0}^{k-1}[(x-a)-ih]\\&=f(a)+\sum _{k=1}^{n}{\frac {\Delta _{h}^{k}[f](a)}{k!}}\prod _{i=0}^{k-1}\left({\frac {x-a}{h}}-i\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acf264500fc988a5ec93afcba6be755b5a7c2acc)
在最終公式中hk被消去掉了,對於非一致步長的情況則不會出現階乘。














}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805521ccbfe6baf45085b5499093e5362c33cb2d)

\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dec48afb9723d70eb6d843de94c7a5069370bfb)
-\Delta ^{n-1}[f](x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e507cab6c570c0f32063759cd143e826adbb9e61)
=\sum _{i=0}^{n}{n \choose i}(-1)^{n-i}f(x+i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/378a9d98e057cb2afcfe03160ed26d7598cf4586)

=f(x+2)-2f(x+1)+f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/002e6ddd14e4ec8068b1d97640ed68e91d1012e3)















+{\frac {x-a-1}{2}}\left(\Delta ^{2}[f](a)+\cdots \right)\right]\\&=f(a)+\sum _{k=1}^{n}\Delta ^{k}[f](a)\prod _{i=1}^{k}{\frac {[(x-a)-i+1]}{i}}\\&=\sum _{k=0}^{n}{x-a \choose k}~\Delta ^{k}[f](a)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaaae992f781f01dc21b5796c9d397a09060b194)




}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bc739bf70fe5e7a770c261da81fe064a8e5f261)


+{\frac {x-a-h}{2h}}\left(\Delta _{h}^{2}[f](a)+\cdots \right)\right]\\&=f(a)+\sum _{k=1}^{n}{\frac {\Delta _{h}^{k}[f](a)}{k!h^{k}}}\prod _{i=0}^{k-1}[(x-a)-ih]\\&=f(a)+\sum _{k=1}^{n}{\frac {\Delta _{h}^{k}[f](a)}{k!}}\prod _{i=0}^{k-1}\left({\frac {x-a}{h}}-i\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acf264500fc988a5ec93afcba6be755b5a7c2acc)