import enum
import itertools
import time
from math import floor, ceil
import numba as nb
import numpy as np
import matplotlib
from PIL import Image, PyAccess
# Amount of times to print the total progress
PROGRESS_STEPS: int = 20
# Set to `True` to plot the shortcut version of the fractal
SHORTCUT: bool = True
# Make all integers critical points
FIX_CRITICAL_POINTS: bool = True
# Width of the image in pixels and aspect ratio
RESOLUTION: int = 1920*1080//4
ASPECT_RATIO: float = 21/9 if FIX_CRITICAL_POINTS else 16/9
# Value of the center pixel
CENTER: complex = 0 + 0j
# Value range of the real part (width of the horizontal axis)
RE_RANGE: float = 10 if FIX_CRITICAL_POINTS else 5
# Show grid lines for integer real and imaginary parts
SHOW_GRID: bool = False
GRID_COLOR: tuple[int, int, int] = (125, 125, 125)
# Matplotlib named colormap
COLORMAP_NAME: str = 'inferno'
# Plot range of the axes
X_MIN = CENTER.real - RE_RANGE/2 # min Re(z)
X_MAX = CENTER.real + RE_RANGE/2 # max Re(z)
Y_MIN = CENTER.imag - RE_RANGE/(2*ASPECT_RATIO) # min Im(z)
Y_MAX = CENTER.imag + RE_RANGE/(2*ASPECT_RATIO) # max Im(z)
x_range = X_MAX - X_MIN
y_range = Y_MAX - Y_MIN
pixels_per_unit = np.sqrt(RESOLUTION/(x_range*y_range))
# Width and height of the image in pixels
WIDTH = round(pixels_per_unit*x_range)
HEIGHT = round(pixels_per_unit*y_range)
# Maximum iterations for the divergence test (recommended >= 60)
MAX_ITER: int = 60
# Max value of Re(z) and Im(z) for which the recursion doesn't overflow
CUTOFF_RE = 7.564545572282618e+153
CUTOFF_IM = 112.10398935569289 if SHORTCUT else 111.95836403625282
# Smallest positive real fixed point
INNER_FIXED_POINT = 0.277733766171606 if SHORTCUT else 0.150108511304474
# Precompute the colormap
CMAP_LEN: int = 2000
cmap_mpl = matplotlib.colormaps[COLORMAP_NAME]
# Start away from 0 (discard black values for the 'inferno' colormap)
# Matplotlib's colormaps have 256 discrete color points
n_cmap = round(256*0.98)
CMAP = [cmap_mpl(k/256) for k in range(256 - n_cmap, 256)]
# Interpolate
x = np.linspace(0, 1, num=CMAP_LEN)
xp = np.linspace(0, 1, num=n_cmap)
c0, c1, c2 = tuple(np.interp(x, xp, [c[k] for c in CMAP]) for k in range(3))
CMAP = []
for x0, x1, x2 in zip(c0, c1, c2):
CMAP.append(tuple(round(255*x) for x in (x0, x1, x2)))
class DivType(enum.Enum):
"""Divergence type."""
CONVERGED = -1 # Converged
MAX_ITER = 0 # Maximum iterations reached
CUTOFF_RE = 1 # Diverged by exceeding the real part cutoff
CUTOFF_IM = 2 # Diverged by exceeding the imaginary part cutoff
@nb.jit(nb.float64(nb.float64, nb.int64), nopython=True)
def smooth(x, k=1):
"""Recursive exponential smoothing function."""
y = np.expm1(np.pi*x)/np.expm1(np.pi)
if k <= 1:
return y
return smooth(y, np.fmin(6, k - 1))
@nb.jit(nb.float64(nb.float64, nb.float64), nopython=True)
def get_delta(x, cutoff):
"""Get the fractional part of the smoothed divergence count."""
nu = np.log(np.abs(x)/cutoff)/(np.pi*cutoff - np.log(cutoff))
nu = np.fmax(0, np.fmin(nu, 1))
return smooth(1 - nu, 2)
@nb.jit(
nb.types.containers.Tuple((
nb.float64,
nb.types.EnumMember(DivType, nb.int64)
))(nb.complex128),
nopython=True
)
def divergence_count(z):
"""Return a smoothed divergence count and the type of divergence."""
z_fix = 0 + 0j
for k in range(MAX_ITER):
c = np.cos(np.pi*z)
if SHORTCUT:
if FIX_CRITICAL_POINTS:
z_fix = (0.5 - c)*np.sin(np.pi*z)/np.pi
z = 0.25 + z - (0.25 + 0.5*z)*c + z_fix
else: # Regular
if FIX_CRITICAL_POINTS:
z_fix = (1.25 - 1.75*c)*np.sin(np.pi*z)/np.pi
z = 0.5 + 1.75*z - (0.5 + 1.25*z)*c + z_fix
if np.abs(z.imag) > CUTOFF_IM:
# Diverged by exceeding the imaginary part cutoff
return k + get_delta(z.imag, CUTOFF_IM), DivType.CUTOFF_IM
if np.abs(z.real) > CUTOFF_RE:
# Diverged by exceeding the real part cutoff
return k + get_delta(z.real, CUTOFF_RE), DivType.CUTOFF_RE
if np.abs(z) < INNER_FIXED_POINT:
# Converged to a fixed point
return -1, DivType.CONVERGED
# Maximum iterations reached
return -1, DivType.MAX_ITER
@nb.jit(nb.float64(nb.float64), nopython=True)
def cyclic_map(g):
"""A continuous function that cycles back and forth from 0 to 1."""
# This can be any continuous function.
# Log scale removes high-frequency color cycles.
freq_div = 12
g = np.log1p(np.fmax(0, (g - 1)/freq_div))
# Beyond this value for float64, decimals are truncated
if g >= 2**51:
return -1
# Normalize and cycle
# g += 0.5 # phase from 0 to 1
return 1 - np.abs(2*(g - np.floor(g)) - 1)
@nb.jit(nb.complex128(nb.types.containers.UniTuple(nb.float64, 2)),
nopython=True)
def pixel_to_z(p):
"""Convert pixel coordinates to its corresponding complex value."""
re = X_MIN + (X_MAX - X_MIN)*p[0]/WIDTH
im = Y_MAX - (Y_MAX - Y_MIN)*p[1]/HEIGHT
return re + 1j*im
class Progress:
"""Simple progress check helper class."""
def __init__(self, n: int, steps: int = 10):
self.n = n
self.k = 0
self.steps = steps
self.step = 1
self.progress = 0
def check(self) -> bool:
self.k += 1
self.progress = self.k/self.n
if self.steps*self.k >= self.step*self.n:
self.step += 1
return True
return self.progress == 1
def create_image():
img = Image.new('RGB', (WIDTH, HEIGHT))
pix = img.load()
pix: PyAccess
n_pix = WIDTH*HEIGHT
prog = Progress(n_pix, steps=PROGRESS_STEPS)
for p in itertools.product(range(WIDTH), range(HEIGHT)):
c = pixel_to_z(p)
g, div_type = divergence_count(c)
if g >= 0:
pix[p] = CMAP[round(cyclic_map(g)*(CMAP_LEN - 1))]
else:
# Color of the interior of the fractal
pix[p] = (0, 0, 0)
if prog.check():
print(f'{prog.progress:<7.1%}')
if SHOW_GRID:
for x in range(ceil(X_MIN), floor(X_MAX) + 1):
px = round((x - X_MIN)*(WIDTH - 1)/(X_MAX - X_MIN))
for py in range(HEIGHT):
pix[(px, py)] = GRID_COLOR
for y in range(ceil(Y_MIN), floor(Y_MAX) + 1):
py = round((Y_MAX - y)*(HEIGHT - 1)/(Y_MAX - Y_MIN))
for px in range(WIDTH):
pix[(px, py)] = GRID_COLOR
return img
img = create_image()
strtime = time.strftime('%Y%m%d-%H%M%S')
fractal_type = 'Shortcut' if SHORTCUT else 'Regular'
filename = f'Collatz_{fractal_type}_{strtime}.png'
img.save(filename)

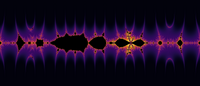
 .[1] The center of the image is
.[1] The center of the image is  and the real part goes from
and the real part goes from  to
to  .
.