传热

热传（heat transfer）有三种方式：

• 热传导（heat conduction）：一个分子向另一个分子传递振动能，使热能从高温向低温部分转移。各种材料的热传导性能不同，传导性能好的，如金属，还包括了自由电子的移动，所以传热速度快，可以做热交换器材料；传导性能不好的，如石棉，可以做热绝缘材料。
• 热对流（heat convection）：是指由于流体的宏观运动而引起的流体各部分之间发生相对位移，冷热流体相互掺混所引起的热量传递过程。不同的温度导致引起系统的密度差是造成对流的原因。对流传导因为牵扯到动力过程，所以比直接传导迅速。
• 热辐射（heat radiation）：是直接通过电磁波辐射向外发散热量，传导速度取决于热源的绝对温度，温度越高，辐射越强。

根据传热的方式和工艺要求，设计热交换器，几乎各种化学工业都有热交换过程，需要各种热交换器。

热传分析

热传递以其所有模式（即传导，对流和辐射）发生，一般运输方程的微分形式如下：

${\frac {\partial {(\rho \phi )}}{\partial t}}+{div\,(\rho u\phi )}={div\,(k\,grad\,\phi )}+{S_{\phi }}$

（1）

可以通过有限差分法（FDM），有限体积法（FVM）和有限元素法（FEM）获得上述方程的数值解。为了进行传热分析，将等式（1）中的标量函数ф替换为温度（T），将扩散系数Γ替换为导热系数k和源项$S_{\phi }$由发热项e或任何热辐射源代替$Q_{i}$或两者兼而有之（取决于可用来源的性质），并且针对不同情况存在不同形式的方程式。为了简单和容易理解，仅讨论了一维情况。

可以通过以下两种方式对物体进行传热分析

1. 稳态热分析
2. 瞬态热分析

稳态热分析

稳态热分析包括以下类型的控制微分方程。

情况1 ：一般稳态导热方程。

在这种情况下，控制微分方程（1）变为：

${div\,(\rho uT)}={div\,(k\,grad\,T)}+{S_{T}}\,$

情况2 ：稳态热传导方程（不产生热量）

在这种情况下，控制方程（1）变为：

${div\,(\rho uT)}={div\,(k\,grad\,T)}\,$

情况3 ：稳态热传导方程（不产生热，不对流）

在这种情况下，控制微分方程（GDE）（1）变为：

${div\,(k\,grad\,T)}=0\,$

瞬态热分析

瞬态热分析包括以下类型的控制微分方程。

情况1 ：瞬态热传导

在这种情况下，控制微分方程（1）变为：

${\frac {\partial {(\rho T)}}{\partial t}}+{div\,(\rho uT)}={div\,(k\,grad\,T)}+{S_{T}}\,$

情况2 ：瞬态热传导（不发热）

在这种情况下，控制微分方程（GDE）（1）变为：

${\frac {\partial {(\rho T)}}{\partial t}}+{div\,(\rho uT)}={div\,(k\,grad\,T)}$

情况3 ：瞬态热传导（不产生热也没有对流）

在这种情况下，控制微分方程（GDE）（1）变为：

${\frac {\partial {(\rho T)}}{\partial t}}={div\,(k\,grad\,T)}\,$

稳态传热分析中控制微分方程的离散化

考虑某物体厚度为L，发热为e，导热系数为k。将物体细分为M个相等的厚度区域$\Delta x$ = x / T沿x方向，距一定间格分割为各节点，如图2所示。

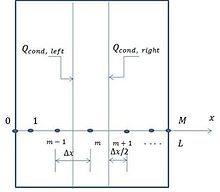图2：平面壁一维传导有限差分公式的节点和体积单元

如图所示，x方向上的整个墙区域按元素划分，所有内部元素的大小相同，而外部元素的大小为一半。

现在，要获得内部节点的有限差分解，请考虑由节点m表示的元素，该元素被相邻节点m-1和m + 1包围。 有限差分技术假定墙壁中的温度线性变化（如图3所示）。

有限差分解决方案是（对于除0和最后一个节点之外的所有内部节点）：

${\frac {(T_{m-1}^{i}-2T_{m}^{n}+T_{m}^{i})}{\Delta {x}^{2}}}+{\frac {e}{k}}=0$

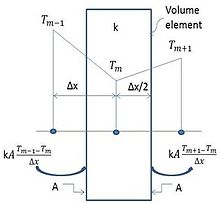图3：有限差分公式中的线性温度变化

边界条件

上式仅对内部节点有效。为了获得外部节点的解决方案，我们必须应用如下边界条件（如适用）。

规定的热通量边界条件

$q_{0}A+kA{\frac {(T_{1}-T_{0})}{\Delta {x}}}+{\frac {e_{0}}{2}}A\Delta {x}=0$

边界绝缘时（q = 0）

$kA{\frac {(T_{1}-T_{0})}{\Delta {x}}}+{\frac {e_{0}}{2}}A\Delta {x}=0$

对流边界条件

$hA{(T_{\infty }-T_{0})}+kA{\frac {(T_{1}-T_{0})}{\Delta {x}}}+{\frac {e_{0}}{2}}A\Delta {x}=0$

辐射边界条件

$\epsilon \sigma A{(T_{sur}^{4}-T_{0}^{4})}+kA{\frac {(T_{1}-T_{0})}{\Delta {x}}}+{\frac {e_{0}}{2}}A\Delta {x}=0$

对流和辐射联合边界条件

$hA{(T_{\infty }-T_{0})}+\epsilon \sigma A{(T_{sur}^{4}-T_{0}^{4})}+kA{\frac {(T_{1}-T_{0})}{\Delta {x}}}+{\frac {e_{0}}{2}}A\Delta {x}=0$

如图4所示，或当将辐射和对流传热系数组合时，上式如下：

$hA_{combined}{(T_{\infty }-T_{0})}+kA{\frac {(T_{1}-T_{0})}{\Delta {x}}}+{\frac {e_{0}}{2}}A\Delta {x}=0\,$

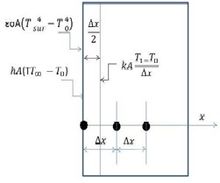图4：平面壁左边界上对流和辐射相结合的有限差分公式的示意图

对流，辐射和热通量边界条件的组合

$q_{0}A+hA{(T_{\infty }-T_{0})}+\epsilon \sigma A{(T_{sur}^{4}-T_{0}^{4})}+kA{\frac {(T_{1}-T_{0})}{\Delta {x}}}+{\frac {e_{0}}{2}}A\Delta {x}=0$

接触面边界条件

在非均质物体，如复合壁中，具有不同热物理特性的不同物质紧密接合在一起。假定两种不同的固体介质A和B完全接触，因此在节点m的界面处具有相同的温度（如图5所示）。

$k_{A}A{\frac {(T_{m-1}-T_{m})}{\Delta {x}}}+k_{B}A{\frac {(T_{m+1}-T_{m})}{\Delta {x}}}+{\frac {e_{A,m}}{2}}A\Delta {x}+{\frac {e_{B,m}}{2}}A\Delta {x}=0$

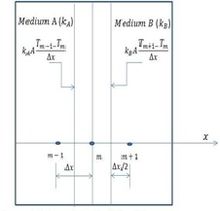图5：两种具有完美热接触的介质A和B的界面边界条件的有限差分示意图

在上式中，

$q_{0}$ =表示指定的热通量在$(W/m^{2})$ ，

h =对流系数，

$h_{combined}$ =对流和辐射的总纯热系数，

$T_{s}ur$ =周围表面的温度，

$T_{(}\infty )$ =环境温度，

$T_{0}$ =初始节点的温度。 $T_{0}$到$T_{l}$之间的热流关系，也可适用于$T_{l}$到$T_{2}$之间；将$T_{0}$到$T_{\infty }$之间的热流串联，便能得经过该复合墙面，从室外到室内的热流。

瞬态传热分析中控制微分方程的离散化

瞬态热分析比稳定热分析更重要，因为该分析包括随时间变化的环境条件。在瞬态热传导中，温度随时间和位置而变化。如图6所示，瞬态热传导的有限差分法解除了空间离散以外，还需要时间步阶离散。

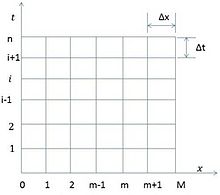图6：有限差分随时间变化的问题涉及时间以及空间上的离散点

如图7所示，存在平面壁中一维传导有限差分法瞬态公式的节点和体积元素。

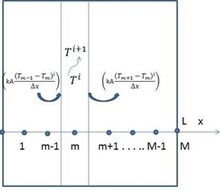图7：平面壁一维瞬态有限差分公式的节点和体积元素

对于这种情况，方程式（1）的有限差分显式解如下：

$kA{\frac {(T_{m-1}^{i}-T_{m}^{i})}{\Delta {x}}}+kA{\frac {(T_{m+1}^{i}-T_{m}^{i})}{\Delta {x}}}+{e_{m}}A\Delta {x}=(\rho c_{p}\Delta xA){\frac {(T_{m}^{i+1}-T_{m}^{i})}{\Delta x}}$

上面的方程可以针对温度明确求解$(T_{m}^{i+1})$给

${T_{m}^{i+1}}=\tau {(T_{m+1}^{i}-T_{m}^{i})}+{(1-2\tau )}T_{m}^{i}+\tau {\frac {(e_{m}\Delta {x}^{2})}{k}}$

此处，

$\tau ={\frac {(\alpha \Delta t)}{\Delta x^{2}}}\,$

和

$\alpha ={\frac {k}{\rho c_{p}}}\,$

这里， $\tau$代表细胞傅立叶号， $\alpha$代表热扩散率$c_{p}$代表恒压下的比热， $\Delta t$代表时间步长， $\Delta x$代表空间步长。

上面的等式对所有内部节点均有效，并找到第一个和最后一个节点的关系，应用边界条件（如适用），如稳态传热中所述。对于对流和辐射边界，如照射物体的太阳辐射 $q_{solar}$ ，单位为 $(W/m^{2})$ ，反照率常数K已知，与温度的关系如下：

$hA{(T_{\infty }^{i}-T_{0}^{i})}+\kappa Aq_{solar}=(\rho c_{p}\Delta xA){\frac {(T_{1}^{i}-T_{0}^{i})}{\Delta x}}$