数值分析与科学计算中,反向欧拉法或隐式欧拉法是求解常微分方程最基本的数值方法之一。其类似于(标准)欧拉法,不过是一种隐式方法。反向欧拉法的时间误差为一阶。
考虑常微分方程

有初值 此处函数
此处函数 与初值数据
与初值数据 、
、 均未知;函数
均未知;函数 取决于实变量
取决于实变量 ,同样未知。数值方法产生一个序列
,同样未知。数值方法产生一个序列 ,使
,使 近似于
近似于 ,其中
,其中 称为步长。
称为步长。
反向欧拉法计算近似值的方法是
 [1]:57
[1]:57
异于(正向)欧拉法,后者用的是 而非
而非 。
。
反向欧拉法是一种隐式方法:新近似值 在方程两侧都出现,因此该方法要求解未知
在方程两侧都出现,因此该方法要求解未知 的代数方程。对非刚性问题,这可采用定点迭代法:
的代数方程。对非刚性问题,这可采用定点迭代法:
![{\displaystyle y_{k+1}^{[0]}=y_{k},\quad y_{k+1}^{[i+1]}=y_{k}+hf(t_{k+1},y_{k+1}^{[i]}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e8e8501d252780d672b65b22097d0b01afdc9c0)
若序列收敛(在给定精度内),则该方法会将其极限作为新的近似
 。[1]:57
。[1]:57
或者,也可以使用牛顿–拉斐森法求解代数方程。
将微分方程 自
自 积分到
积分到 ,有
,有

现在用右手矩形法近似计算右式的积分:

最后,用 应近似于
应近似于 的性质,就得到了反向欧拉法公式。[1]:57
的性质,就得到了反向欧拉法公式。[1]:57
若用左手矩形法,同样的推导会得到(标准)欧拉法。
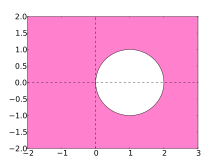 圆盘外的粉色区域是反向欧拉法的稳域。
圆盘外的粉色区域是反向欧拉法的稳域。
用大O符号表示反向欧拉法的局部截断误差(LTE)(定义为迭代一步产生的误差)为 。特定时刻
。特定时刻 的误差为
的误差为 ,这是说该方法的阶数为1。一般来说,具有
,这是说该方法的阶数为1。一般来说,具有 LTE的方法定义为k阶。
LTE的方法定义为k阶。
反向欧拉法的绝对稳域是以1为圆心,半径为1的圆盘在平面内的补集,如图所示。[1]:70这包括整个复平面的左半部,使其适于求解刚性方程。[1]:71事实上,反向欧拉法甚至是L-稳定的。
利用反向欧拉法求解离散稳定系统的区域是半径为0.5的圆,位于z平面的(0.5, 0)处。[2]
反向欧拉法是(前向)欧拉法的一种变体。其他变体还有半隐式欧拉法和指数欧拉法。
反向欧拉法可视为1阶段的龙格-库塔法,可用Butcher表描述:

该方法也可看作是1步的线性多步法,是Adams–Moulton法族中的第一个方法,也是后向微分法的第一个方法。
- ^ 1.0 1.1 1.2 1.3 1.4 Butcher 2003
- ^ Wai-Kai Chen, Ed., Analog and VLSI Circuits The Circuits and Filters Handbook, 3rd ed. Chicago, USA: CRC Press, 2009.

















![{\displaystyle y_{k+1}^{[0]}=y_{k},\quad y_{k+1}^{[i+1]}=y_{k}+hf(t_{k+1},y_{k+1}^{[i]}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e8e8501d252780d672b65b22097d0b01afdc9c0)








